Group without torsion

torsion-free group

A group without non-trivial elements of finite order. Free, free solvable, free nilpotent, and free Abelian groups are torsion-free groups (cf. Free Abelian group; Free group; Nilpotent group; Solvable group). Direct, complete direct and free products (cf. Direct product; Free product of groups) of torsion-free groups are torsion-free. The quotient group of a torsion-free group 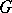by a normal subgroup 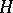is a torsion-free group if and only if 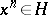implies 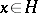for all 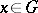and for any natural number . An extension of a torsion-free group by a torsion-free group is a torsion-free group. 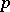If a group is residually a finite -group (cf. Residually-finite group; 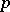-group) with respect to two different prime numbers 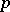, then it is a torsion-free group.

References

[1]	A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian)