Engel group

A group 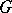in which for every two elements 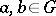there is an integer 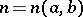such that 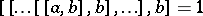, where 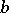is separated times and 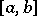is the commutator of and 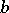. If this number can be chosen independently of and 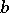, then 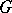is called an Engel group of finite class . The class of Engel groups contains that of locally nilpotent groups, but does not coincide with it. Every nilpotent group of class is an Engel group of the same class. Engel groups of class 2 are nilpotent of class at most 3.

They are named after F. Engel.

References

[1]	A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian)

Comments

A finite Engel group is nilpotent (cf. Nilpotent group).

References

[a1]	D.J.S. Robinson, "A course in the theory of groups" , Springer (1982)
[a2]	B. Huppert, "Finite groups" , 3 , Springer (1982)