Delta-function method

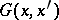A method for finding the Green function of a linear differential equation in mathematical physics (i.e. a method for determining the function of the effect of a point source) with the aid of the delta-function . The Green function of a linear differential operator is defined by the equation

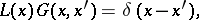or 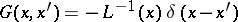, i.e. it expresses the effect of a point source located at the point 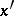on the value of the resulting perturbation at the point . The form of the inverse operator 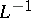is most simply determined in the frequently occurring case when 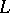is a differential operator with constant coefficients (independent of ). The solution of a non-homogeneous linear differential equation of a general type for a perturbation 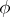with source ,

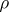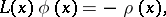is described with the aid of the Green function as the convolution

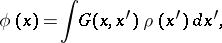the integration being effected over the entire domain of action of the source .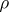

References

[1]	D. Ivanenko, A. Sokolov, "Classical field theory" , Mosow-Leningrad (1951) (In Russian)

References

[a1]	P.M. Morse, H. Feshbach, "Methods of theoretical physics" , 1–2 , McGraw-Hill (1953)