Quasi-regular ring

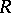A ring in which every element is quasi-regular. An element of an alternative (in particular, associative) ring is called quasi-regular if there is an element 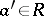such that

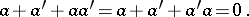The element 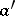is called the quasi-inverse of . If 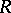is a ring with identity 1, then an element 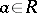is quasi-regular with quasi-inverse 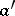if and only if the element 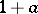is invertible in 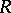with inverse 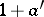. Every nilpotent element is quasi-regular. In an associative ring the set of all quasi-regular elements forms a group with respect to the operation of cyclic composition: 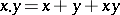. An important example of a quasi-regular ring is the ring of (non-commutative) formal power series without constant terms. There exist simple associative quasi-regular rings [2].

References

[1]	N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956)
[2]	E. Sasiada, P.M. Cohn, "An example of a simple radical ring" J. of Algebra , 5 : 3 (1967) pp. 373–377