Cissoid

A plane algebraic curve of order three whose equation in Cartesian coordinates is

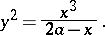The parametric equations are

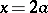A cissoid is symmetric relative to the -axis (Fig.). The coordinate origin is a cusp, the asymptote is . The area between the curve and the asymptote is .

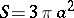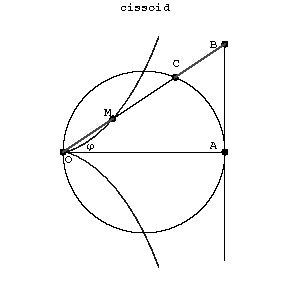
Figure: c022340a

The cissoid is often called the cissoid of Diocles in honour of the Ancient Greek mathematician Diocles (3rd century B.C.), who discussed it in connection with the problem of duplication of the cube.

The cissoid is the set of points 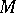for which 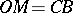, where 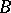and 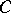are the points of intersection of the line 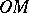with a circle and the tangent 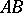to the circle at the point 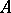diametrically opposite to 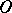. If in this construction one replaces the circle and straight line by curves 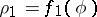and , then the resulting curve 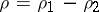is called a cissoidal curve, or the cissoid of the (given) curves.

References

[1]	A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)
[2]	A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian)

References

[a1]	J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972)
[a2]	E. Brieskorn, H. Knörrer, "Ebene algebraische Kurven" , Birkhäuser (1981)