Cone condition
A condition on a region of Euclidean space expressing some non-flatness property. An open set 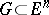 satisfies the weak cone condition if
satisfies the weak cone condition if 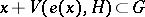 for all
for all 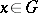 , where
, where 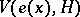 is a right circular cone with vertex at the origin of fixed opening
is a right circular cone with vertex at the origin of fixed opening  and height
and height 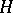 ,
, 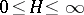 , and with axis vector
, and with axis vector 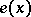 depending on
depending on  . An open set
. An open set 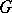 satisfies the strong cone condition if there exists a covering of the closure
satisfies the strong cone condition if there exists a covering of the closure 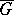 by open sets
by open sets 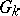 such that for any
such that for any 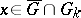 the cone
the cone 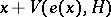 is contained in
is contained in 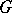 (the openings of these cones may depend on
(the openings of these cones may depend on 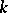 ). In connection with integral representations of functions and imbedding theorems, anisotropic generalizations of cone conditions have been considered, for example, the weak and strong
). In connection with integral representations of functions and imbedding theorems, anisotropic generalizations of cone conditions have been considered, for example, the weak and strong 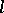 -horn conditions (see [1]), the cube condition, etc.
-horn conditions (see [1]), the cube condition, etc.
References
| [1] | O.V. Besov, V.P. Il'in, S.M. Nikol'skii, "Integral representations of functions and imbedding theorems" , Wiley (1978) (Translated from Russian) |
Comments
References
| [a1] | S. Agmon, "Lectures on elliptic boundary value problems" , v. Nostrand (1965) |
Cone condition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cone_condition&oldid=31912