Symmetry test
A statistical test for testing the hypothesis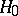 
that a one-dimensional probability density is symmetric about zero.
Let the hypothesis of symmetry 
be that the probability density 
of the probability law of independent random variables 
is symmetric about zero, that is,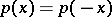 
for any 
from the domain of definition of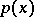 
. Any statistical test intended for testing 
is called a symmetry test.
Most often the hypothesis 
that all the random variables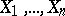 
have probability density 
, 
, is considered as the alternative to 
. In other words, according to 
the probability density of 
is obtained by shifting the density 
along the 
-axis by a distance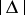 
, to the right or left according to the sign of 
. If the sign of the displacement 
is known, then 
is called one-sided, otherwise it is called two-sided. A simple example of a symmetry test is given by the sign test.
Usually a randomization test is used for testing symmetry.
References
| [1] | Z. Sidak, "Theory of rank tests" , Acad. Press (1967) |
| [2] | M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 2. Inference and relationship , Griffin (1979) |
Symmetry test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetry_test&oldid=31876