Path space
From Encyclopedia of Mathematics
The space 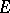 of the fibre space
of the fibre space 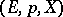 , which is called the path fibre space. Here
, which is called the path fibre space. Here 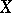 is a path-connected space with a distinguished point
is a path-connected space with a distinguished point  ,
, 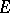 is the set of paths (cf. Path) in
is the set of paths (cf. Path) in 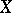 starting from
starting from  and
and 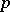 is the mapping associating to each path its end-point. Moreover,
is the mapping associating to each path its end-point. Moreover, 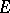 is considered to have the compact-open topology. The fibre of this fibre space (which is a Serre fibration) is the loop space
is considered to have the compact-open topology. The fibre of this fibre space (which is a Serre fibration) is the loop space 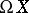 — the set of all loops (cf. Loop) in
— the set of all loops (cf. Loop) in 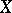 at
at  . A path space can be contracted within itself to a point, so the homotopy groups
. A path space can be contracted within itself to a point, so the homotopy groups 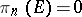 , and the homotopy sequence of the path fibre space degenerates into the so-called Hurewicz isomorphisms:
, and the homotopy sequence of the path fibre space degenerates into the so-called Hurewicz isomorphisms:
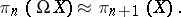 |
Comments
References
| [a1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. 75ff, 99ff |
How to Cite This Entry:
Path space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Path_space&oldid=31871
Path space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Path_space&oldid=31871
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article