Bell numbers
From Encyclopedia of Mathematics
The Bell numbers 
are given by
 |
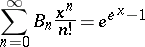or by
 |
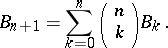Also,
 |
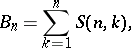where 
are Stirling numbers (cf. Combinatorial analysis) of the second kind, so that 
is the total number of partitions of an 
-set.
They are equal to 
.
The name honours E.T. Bell.
References
| [a1] | L. Comtet, "Advanced combinatorics" , Reidel (1974) |
How to Cite This Entry:
Bell numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bell_numbers&oldid=31865
Bell numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bell_numbers&oldid=31865
This article was adapted from an original article by N.J.A. Sloane (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article