Search problem (linear)

An optimality problem first formulated by R. Bellman [a1]. Suppose a particle is located on the real line, its unknown position being characterized by a symmetric probability distribution 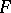. A searcher starts at the origin and can move in either direction with constant velocity until the target is found. The problem is to determine a path which minimizes the expected searching time.

W. Franck [a2] showed that there exist paths with finite expected searching time if and only if 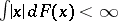. Sufficient conditions for the existence of an optimal search path were established by A. Beck (in [a3] and subsequent papers in Israel J. Math.). Optimal search paths were constructed [a4] for the distributions of Gauss, Laplace and Student. A recent survey of the linear search problem, including generalizations and open questions, can be found in [a5].

References

[a1]	R. Bellman, "Research problem No. 63–9" SIAM Review , 5 (1963) pp. 274
[a2]	W. Franck, "An optimal search problem" SIAM Review , 7 (1965) pp. 503–512
[a3]	A. Beck, "On the linear search problem" Israel J. Math. , 2 (1964) pp. 221–228
[a4]	P.J. Rousseeuw, "Optimal search paths for random variables" J. Comput. Appl. Math. , 9 (1983) pp. 279–286
[a5]	F.T. Bruss, J.B. Robertson, "A survey of the linear search problem" Math. Scientist , 13 (1988) pp. 75–89