Condensation point
See Condensation point of a set; Limit point of a set; Accumulation point.
Comments
The three notions mentioned above should be clearly distinguished. If 
is a subset of a topological space 
and 
is a point of 
, then 
is an accumulation point of 
if and only if every neighbourhood of 
intersects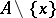 
. It is a condensation point of 
if and only if every neighbourhood of it contains uncountably many points of 
.
The term limit point is slightly ambiguous. One might call 
a limit point of 
if every neighbourhood of 
contains infinitely many points of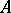 
, but this is not standard. Sometimes one calls 
a limit point of a net (cf. Net (of sets in a topological space)) if some subset of this net converges to 
. However, most people call 
a cluster point in this case.
In the case of a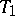 
-space 
the notions of a limit point of a set 
and an accumulation point of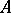 
coincide, and one uses "accumulation point" .
Condensation point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Condensation_point&oldid=31858