Alternating group
From Encyclopedia of Mathematics
of degree 
The subgroup  of the symmetric group
of the symmetric group  consisting of all even permutations.
consisting of all even permutations.  is a normal subgroup in
is a normal subgroup in  of index 2 and order
of index 2 and order  . The permutations of
. The permutations of  , considered as permutations of the indices of variables
, considered as permutations of the indices of variables  , leave the alternating polynomial
, leave the alternating polynomial  invariant, hence the term "alternating group" . The group
invariant, hence the term "alternating group" . The group  may also be defined for infinite cardinal numbers
may also be defined for infinite cardinal numbers 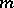 , as the subgroup of
, as the subgroup of 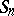 consisting of all even permutations. If
consisting of all even permutations. If  , the group
, the group 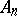 is
is 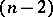 -fold transitive. For any
-fold transitive. For any  , finite or infinite, except
, finite or infinite, except  , this group is simple; this fact plays an important role in the theory of solvability of algebraic equations by radicals.
, this group is simple; this fact plays an important role in the theory of solvability of algebraic equations by radicals.
References
| [1] | M. Hall, "Group theory" , Macmillan (1959) |
Comments
Note that 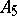 is the non-Abelian simple group of smallest possible order.
is the non-Abelian simple group of smallest possible order.
How to Cite This Entry:
Alternating group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Alternating_group&oldid=31834
Alternating group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Alternating_group&oldid=31834
This article was adapted from an original article by N.N. Vil'yams (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article