Euclidean field
From Encyclopedia of Mathematics
An ordered field in which every positive element is a square. For example, the field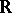 
of real numbers is a Euclidean field. The field 
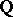of rational numbers is not a Euclidean field.
Comments
There is a second meaning in which the phrase Euclidean field is used (especially for quadratic number fields). A number field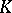 
(i.e. a finite field extension of 
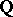) is called Euclidean if its ring of integers 
is a Euclidean ring. The Euclidean quadratic fields 
, 
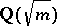a square-free integer, are precisely the fields with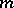 
equal to 
, 
, 
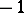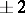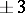, 5, 6, 
, 
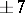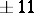, 13, 17, 19, 21, 29, 33, 37, 41, 57, or 73, cf. [a1], Chapt. VI.
References
| [a1] | E. Weiss, "Algebraic number theory" , McGraw-Hill (1963) |
How to Cite This Entry:
Euclidean field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euclidean_field&oldid=31825
Euclidean field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euclidean_field&oldid=31825
This article was adapted from an original article by V.L. Popov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article