Discrete measure
From Encyclopedia of Mathematics
A measure concentrated on a set which is at most countable. More generally, let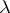 
and 
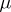be measures (usually with alternating signs) defined on a semi-ring of sets (with its 
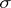-ring of measurable sets). The measure 
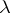is said to be a discrete measure with respect to the measure 
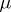if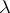 
is concentrated on a set of 
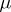-measure zero which is at most countable and any one-point subset of which is 
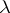-measurable. For instance, the discrete Lebesgue–Stieltjes measure 
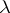of linear sets is equal on half-intervals to the increment of some jump function, which is of bounded variation if 
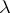is bounded, and which is non-decreasing if 
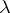is non-negative.
References
| [1] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
How to Cite This Entry:
Discrete measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Discrete_measure&oldid=31791
Discrete measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Discrete_measure&oldid=31791
This article was adapted from an original article by A.P. Terekhin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article