Approximately-compact set
From Encyclopedia of Mathematics
A set having the property of approximate compactness. A metric projection on any approximately-compact Chebyshev set is continuous. Examples of approximately-compact sets include boundedly-compact sets and closed convex sets in the spaces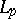 
(
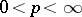), and the set of rational fractions in which the degrees of the numerator and denominator are constant. In approximation theory and in the theory of ill-posed problems frequent use is made of spaces in which all closed sets are approximately compact.
References
| [1] | N.V. Efimov, S.B. Stechkin, "Approximative compactness and Čebyšev sets" Soviet Math. Dokl. , 2 : 5 (1961) pp. 1226–1228 Dokl. Akad. Nauk SSSR , 140 : 3 (1961) pp. 522–524 |
| [2] | L.P. Vlasov, "Approximative properties of sets in normed linear spaces" Russian Math. Surveys , 28 : 6 (1973) pp. 1–66 Uspekhi Mat. Nauk , 28 : 6 (1973) pp. 3–66 |
How to Cite This Entry:
Approximately-compact set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximately-compact_set&oldid=31781
Approximately-compact set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximately-compact_set&oldid=31781
This article was adapted from an original article by Yu.N. Subbotin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article