Approximate compactness

A property of a set 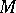in a metric space 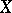requiring that for any 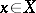, every minimizing sequence 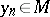(i.e. a sequence with the property 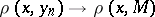) has a limit point 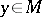. Approximate compactness of a given set ensures the existence of an element of best approximation for any 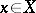. The concept of approximate compactness was introduced [1] in connection with the study of Chebyshev sets (cf. Chebyshev set) in a Banach space, which made it possible to describe convex Chebyshev sets in certain spaces. In fact, let 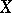be a uniformly-convex smooth Banach space. For a Chebyshev set 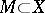to be convex, it is necessary and sufficient that it be approximately compact. It follows, in particular, that the set of rational fractions with fixed degrees of the numerator and the denominator is not a Chebyshev set in the space 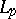(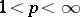) if the degree of the denominator is not smaller than one [1].

For subsequent studies on this subject see [2].

References

[1]	N.V. Efimov, S.B. Stechkin, "Approximative compactness and Čebyšev sets" Soviet Math. Dokl. , 2 : 5 (1961) pp. 522–524 Dokl. Akad. Nauk SSSR , 140 : 3 (1961) pp. 522–524
[2]	A.L. Garkavi, "The theory of best approximation in normed linear spaces" Itogi Nauk. Mat. Anal. 1967 (1969) pp. 75–132 (In Russian)