Lattice with complements
complemented lattice
A lattice 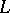 with a zero 0 and a unit 1 in which for any element
with a zero 0 and a unit 1 in which for any element  there is an element
there is an element 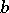 (called a complement of the element
(called a complement of the element  ) such that
) such that 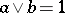 and
and 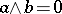 . If for any
. If for any 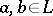 with
with 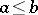 the interval
the interval 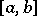 is a complemented lattice, then
is a complemented lattice, then 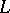 is called a relatively complemented lattice. Each complemented modular lattice is a relatively complemented lattice. A lattice
is called a relatively complemented lattice. Each complemented modular lattice is a relatively complemented lattice. A lattice 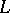 with a zero 0 is called: a) a partially complemented lattice if each of its intervals of the form
with a zero 0 is called: a) a partially complemented lattice if each of its intervals of the form 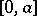 ,
, 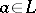 , is a complemented lattice; b) a weakly complemented lattice if for any
, is a complemented lattice; b) a weakly complemented lattice if for any 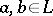 with
with  there is an element
there is an element  such that
such that 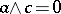 and
and 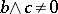 ; c) a semi-complemented lattice if for any
; c) a semi-complemented lattice if for any 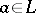 ,
, 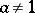 , there is an element
, there is an element 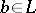 ,
, 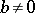 , such that
, such that 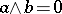 ; d) a pseudo-complemented lattice if for any
; d) a pseudo-complemented lattice if for any 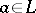 there is an element
there is an element 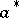 such that
such that 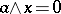 if and only if
if and only if 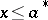 ; and e) a quasi-complemented lattice if for any
; and e) a quasi-complemented lattice if for any 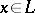 there is an element
there is an element 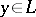 such that
such that 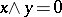 and
and 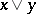 is a dense element. Ortho-complemented lattices also play an important role (see Orthomodular lattice). See [4] for the relation between the various types of complements in lattices.
is a dense element. Ortho-complemented lattices also play an important role (see Orthomodular lattice). See [4] for the relation between the various types of complements in lattices.
References
| [1] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [2] | L.A. Skornyakov, "Elements of lattice theory" , A. Hilger (1977) (Translated from Russian) |
| [3] | L.A. Skornyakov, "Complemented modular lattices and regular rings" , Oliver & Boyd (1964) (Translated from Russian) |
| [4] | P.A. Grillet, J.C. Varlet, "Complementedness conditions in lattices" Bull Soc. Roy. Sci. Liège , 36 : 11–12 (1967) pp. 628–642 |
Comments
In a distributive lattice, each element has at most one complement; conversely, a lattice in which each element has at most one relative complement in each interval in which it lies must be distributive.
References
| [a1] | L. Beran, "Orthomodular lattices" , Reidel (1985) |
| [a2] | G. Grätzer, "Lattice theory" , Freeman (1971) |
| [a3] | M.L. Dubreil-Jacotin, L. Lesieur, R. Croiset, "Leçons sur la théorie des treilles" , Gauthier-Villars (1953) |
Lattice with complements. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lattice_with_complements&oldid=31771