Decidable predicate
From Encyclopedia of Mathematics
An 
-place predicate 
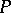given on a certain set of constructive objects (for example, natural numbers) 
for which there exists an algorithm which enables one to find the value (T or F) of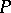 
on any 
-tuple 
of elements in 
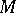. In other words, a predicate is decidable if, regarded as an 
-place function on 
with values in the set 
, it is a computable function.
When the concept of a recursive function or some equivalent concept is used as a mathematical refinement of the concept of computability, then the term "recursive predicaterecursive predicate" is usually employed instead of "decidable predicate" .
Comments
So,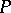 
is a decidable predicate if the set of 
-tuples on which 
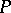takes the value T (true) is a decidable set.
How to Cite This Entry:
Decidable predicate. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Decidable_predicate&oldid=31759
Decidable predicate. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Decidable_predicate&oldid=31759
This article was adapted from an original article by V.E. Plisko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article