Dual algebra
A topological algebra in which, for any closed left (right) ideal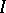 
, the left annihilator of the right (correspondingly, the right annihilator of the left) annihilator of 
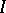is identical with 
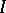. Of greatest interest are the problems of realization of dual algebras as operator algebras and the establishment of connections between the properties of annihilation and duality of topological algebras of different classes, in particular complex Banach algebras with involution, including Hilbert algebras and 
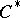-algebras (cf. also Banach algebra; Hilbert algebra; 
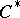-algebra).
The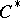 
-algebra of completely-continuous linear operators on a Hilbert space and the Hilbert algebra of Hilbert–Schmidt operators on a Hilbert space are dual algebras. Any dual Banach algebra which is a 
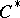-algebra is isomorphic to the completion of a direct algebraic sum of algebras of completely-continuous operators on certain Hilbert spaces. All complete Hilbert algebras are dual; they are isomorphic to the direct orthogonal sum of the Hilbert algebras of Hilbert–Schmidt operators on certain Hilbert spaces. Any semi-simple dual algebra with continuous quasi-inverses is the completion of the direct sum of all its minimal closed two-sided ideals, which are topologically simple dual algebras. A topologically simple dual algebra 
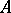may be realized as the algebra of continuous linear operators on some topological vector space 
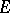containing the set 
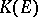of finite-dimensional continuous linear operators on 
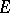; if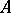 
is a Banach algebra, the image of 
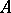in this realization is contained in the uniform closure 
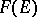of the algebra 
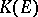. On the other hand, there exists a reflexive Banach space 
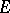such that the (topologically simple, annihilator) Banach algebra 
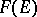is not dual.
References
| [1] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [2] | A.M. Davie, "A counterexample on dual Banach algebras" Bull. London Math. Soc. , 5 : 1 (1973) pp. 79–80 |
Comments
The phrase "dual algebra" is also used in the sense of the dual algebra of a co-algebra; cf. (the editorial comments to) Co-algebra.
Dual algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dual_algebra&oldid=31736