Completely-reducible module
A module 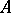 over an associative ring
over an associative ring 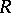 which can be represented as the sum of its irreducible
which can be represented as the sum of its irreducible 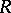 -submodules (cf. Irreducible module). Equivalent definitions are: 1)
-submodules (cf. Irreducible module). Equivalent definitions are: 1) 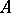 is the sum of its minimal submodules; 2)
is the sum of its minimal submodules; 2) 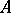 is isomorphic to a direct sum of irreducible modules; or 3)
is isomorphic to a direct sum of irreducible modules; or 3) 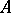 coincides with its socle. A submodule and a quotient module of a completely-reducible module are also completely reducible. The lattice of submodules of a module
coincides with its socle. A submodule and a quotient module of a completely-reducible module are also completely reducible. The lattice of submodules of a module 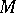 is a lattice with complements if and only if
is a lattice with complements if and only if 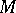 is completely reducible.
is completely reducible.
If all right 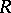 -modules over a ring
-modules over a ring 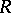 are completely reducible, all left
are completely reducible, all left 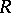 -modules are completely reducible as well, and vice versa;
-modules are completely reducible as well, and vice versa; 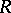 is then said to be a completely-reducible ring or a classical semi-simple ring. For a ring
is then said to be a completely-reducible ring or a classical semi-simple ring. For a ring 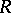 to be completely reducible it is sufficient for it to be completely reducible when regarded as a left (right) module over itself.
to be completely reducible it is sufficient for it to be completely reducible when regarded as a left (right) module over itself.
References
| [1] | J. Lambek, "Lectures on rings and modules" , Blaisdell (1966) |
| [2] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
Completely-reducible module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Completely-reducible_module&oldid=31723