Nil group

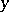A group in which any two elements and are connected by a relation

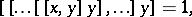where the square brackets denote the commutator

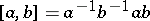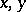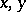and the number of commutators in the definition depends, generally speaking, on the pair . When is bounded for all in the group, the group is called an Engel group. Every locally nilpotent group is a nil group. The converse is not true, in general, but it is under some additional assumptions, for example, when the group is locally solvable (cf. Locally solvable group).

Occasionally the term "nil group" is used in a different meaning. Namely, a nil group is a group in which every cyclic subgroup is subnormal, that is, occurs in some subnormal series of the group (see Normal series of a group).

References

[1]	A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian)

Comments

In [a1] it has been proved that there are periodic Engel groups that are not locally nilpotent.

References

[a1]	E.S. Golod, "On nil-algebras and residually finite 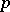-groups" Transl. Amer. Math. Soc. , 48 (1965) pp. 103–106 Izv. Akad. Nauk SSSR Ser. Mat. , 28 (1964) pp. 273–276