Wandering set
From Encyclopedia of Mathematics
The set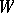 
of all wandering points (cf. Wandering point) of some dynamical system 
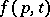. Since for each point 
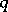the set 
contains all points of the neighbourhood 
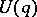, it is open in the phase space 
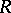. Accordingly, the set 
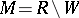of all non-wandering points is closed. The sets 
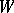and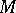 
are invariant, i.e. with each of their points 
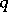they contain the point 
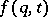for an arbitrary 
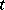. In a compact space 
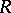each wandering point 
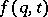tends to 
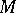both when 
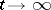and when 
.
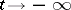References
| [1] | G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. (1927) |
| [2] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [3] | K.S. Sibirskii, "Introduction to topological dynamics" , Noordhoff (1975) (Translated from Russian) |
Comments
References
| [a1] | S. Smale, "Differentiable dynamical systems" Bull. Amer. Math. Soc. , 73 (1967) pp. 747–817 |
| [a2] | N.P. Bhatia, G.P. Szegö, "Stability theory of dynamical systems" , Springer (1970) pp. 30–36 |
How to Cite This Entry:
Wandering set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wandering_set&oldid=31719
Wandering set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wandering_set&oldid=31719
This article was adapted from an original article by K.S. Sibirskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article