Logical formula

An expression in the language of formal logic. An exact definition of a logical formula is given for each specific logical language. As a rule, the definition of a formula has an inductive character: one distinguishes a class of statements, called atomic formulas, and states rules that make it possible to construct new formulas from formulas already constructed, using the symbols for logical operations (cf. Logical operation). For example, the formulas of propositional logic are defined as follows. Any propositional variable is an (atomic) formula. 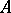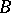If and are formulas, then 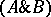, , 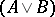, 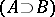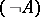are formulas. The formulas of predicate logic are constructed from propositional, predicate and object variables by using logical connectives, quantifiers and auxiliary symbols (brackets and commas). Atomic formulas are propositional variables and expressions of the form 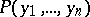, where 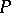is an -place predicate variable and are object variables. The formulas of predicate calculus are defined as follows: a) any atomic formula is a formula; and b) if 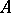and 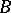are formulas and 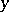is an object variable, then 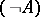, , 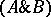, , 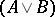, 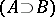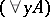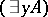are formulas.

Comments

The term "well-formed formulawell-formed formula" (sometimes abbreviated to "wffwff" or "wfwf" ) is in fairly common use.

References

[a1]	A. Grzegorczyk, "An outline of mathematical logic" , Reidel (1974)