Logical consequence

of a given set of premises

A proposition that is true for any interpretation of the non-logical symbols (that is, the names (cf. Name) of objects, functions, predicates) for which the premises are true. If a proposition 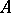is a logical consequence of a set of propositions 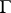, one says that 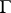logically implies 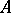, or that 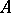follows logically from .

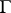If 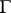is a set of statements of a formalized first-order logico-mathematical language (cf. Logico-mathematical calculus) and 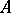is a proposition of this language, then the relation "A is a logical consequence of G" means that any model for 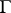is a model for 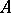. This relation is denoted by 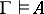. 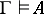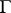The Gödel completeness theorem of classical predicate calculus implies that the relation coincides with the relation , that is, if and only if is deducible from by the methods of classical predicate calculus.

References

[1]	H. Rasiowa, "The mathematics of metamathematics" , Polska Akad. Nauk (1963)
[2]	K. Gödel, "Die Vollständigkeit der Axiome des logischen Funktionenkalküls" Monatsh. Math. Phys. , 37 (1930) pp. 349–360

Comments

The phrase "semantic entailmentsemantic entailment" is sometimes used instead of "logical consequence" ; thus, the expression is read as "G semantically entails A" . The expression 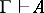is similarly read as "G syntactically entails A" .

References

[a1]	P.T. Johnstone, "Notes on logic and set theory" , Cambridge Univ. Press (1987)
[a2]	A. Grzegorczyk, "An outline of mathematical logic" , Reidel (1974)