Hilbert infinite hotel

Hilbert paradox, infinite hotel paradox, Hilbert hotel

A nice illustration of some of the simpler properties of (countably) infinite sets.

An infinite hotel with rooms numbered 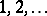can be full and yet have a room for an additional guest. Indeed, simply shift the existing guest in room 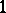to room , the one in room to room , etc. (in general, the one in room to room 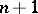), to free room 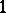for the newcomer.

There is also room for an infinity of new guests. Indeed, shift the existing guest in room 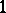to room , the one in room to room 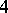, etc. (in general, the one in room to room 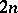), to free all rooms with odd numbers for the newcomers.

These examples illustrate that an infinite set can be in bijective correspondence with a proper subset of itself. This property is sometimes taken as a definition of infinity (the Dedekind definition of infinity; see also Infinity).

References

[a1]	H. Hermes, W. Markwald, "Foundations of mathematics" H. Behnke (ed.) et al. (ed.) , Fundamentals of Mathematics , 1 , MIT (1986) pp. 3–88 (Edition: Third)
[a2]	G.W. Erickson, J.A. Fossa, "Dictionary of paradox" , Univ. Press Amer. (1998) pp. 84
[a3]	L. Radhakrishna, "History, culture, excitement, and relevance of mathematics" Rept. Dept. Math. Shivaji Univ. (1982)