Degree of a point
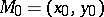 relative to a circle
relative to a circle
 |
with centre at a point 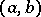
The number
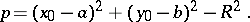 |
One has 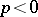 if
if 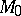 lies within the circle;
lies within the circle; 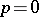 if
if 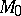 lies on the circle;
lies on the circle; 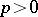 if
if 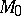 lies outside the circle. The degree of
lies outside the circle. The degree of 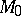 relative to a circle can be represented as the product of the vectors
relative to a circle can be represented as the product of the vectors 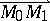 and
and 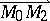 , where
, where 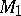 and
and 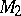 are the points of intersection of the circle and an arbitrary straight line passing through
are the points of intersection of the circle and an arbitrary straight line passing through 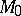 . In particular, the degree of a point
. In particular, the degree of a point 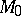 relative to a circle is equal to the square of the length of the tangent drawn from
relative to a circle is equal to the square of the length of the tangent drawn from 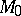 to the circle.
to the circle.
The set of all circles in the plane relative to which a given point has an identical degree forms a net of circles. The set of points of identical degree relative to two non-concentric circles forms a radical axis.
The degree of a point relative to a sphere is defined in the same way. The set of all spheres relative to which a given point has identical degree is called a web of spheres. The set of all spheres relative to which the points of a straight line (the radical axis) have identical degree (different for different points) forms a net of spheres. The set of all spheres relative to which the points of a plane (the radical plane) have identical degree (different for different points) forms a bundle of spheres.
Comments
Customarily this notion is called the power of the point 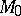 relative to the circle
relative to the circle 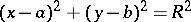 .
.
References
| [a1] | J.L. Coolidge, "A treatise on the circle and the sphere" , Clarendon Press (1916) |
Degree of a point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degree_of_a_point&oldid=31693