Normal complex
From Encyclopedia of Mathematics
of a semi-group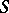 
A non-empty subset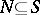 
satisfying the following condition: For any 
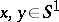(where 
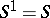when 
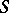contains a unit element and 
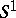is the semi-group obtained from 
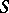by adjoining a unit element if 
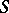does not have one) and any 
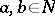it follows from 
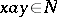that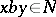 
. A subset 
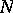is a normal complex of a semi-group 
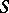if and only if 
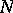is a class of some congruence on 
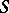(cf. Congruence (in algebra)).
References
| [1] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
How to Cite This Entry:
Normal complex. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_complex&oldid=31680
Normal complex. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_complex&oldid=31680
This article was adapted from an original article by L.N. Shevrin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article