Hilbert cube
From Encyclopedia of Mathematics
The subspace of the Hilbert space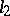 
consisting of all the points 
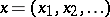for which 
, 
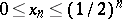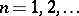. The Hilbert cube is a compactum and is topologically equivalent (homeomorphic) to the Tikhonov product of a countable system of intervals, i.e. to the Tikhonov cube 
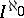. It is a universal space in the class of metric spaces with a countable base (Urysohn's metrization theorem).
Comments
The topology of the Hilbert cube is studied in the field of infinite-dimensional topology (cf. Infinite-dimensional space). This is a rich and fruitful area of investigation.
See [a1] for an excellent introduction and references.
References
| [a1] | J. van Mill, "Topology; with an introduction to infinite-dimensional spaces" , North-Holland (1988) |
How to Cite This Entry:
Hilbert cube. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert_cube&oldid=31650
Hilbert cube. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert_cube&oldid=31650
This article was adapted from an original article by B.A. Pasynkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article