Convex subgroup

A subgroup 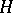of a (partially) ordered group 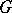which is a convex subset of 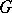with respect to the given order relation. Normal convex subgroups are exactly the kernels of homomorphisms of the partially ordered group which preserve the order. A subgroup of an orderable group which is convex for any total order is called an absolutely convex subgroup; if it is convex only for a certain total order, it is called a relatively convex subgroup. The intersection of all non-trivial relatively convex subgroups of an orderable group is an absolutely convex subgroup; the union of all proper relatively convex subgroups is also an absolutely convex subgroup. Torsion-free Abelian groups have no non-trivial absolutely convex subgroups. A subgroup 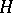of a completely ordered group 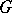is absolutely convex if and only if for any elements 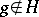, 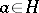the intersection 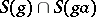is non-empty, where 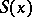is the minimal invariant sub-semi-group of 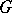containing . 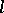A convex -subgroup 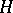of a lattice-ordered group is isolated, i.e. 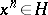for any natural number , it follows from that .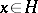

References

[1]	A.I. Kokorin, V.M. Kopytov, "Fully ordered groups" , Israel Program Sci. Transl. (1974) (Translated from Russian)
[2]	L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963)