Diagonal ring

of a closed symmetric algebra 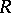of bounded linear operators on a Hilbert space

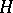A commutative symmetric Banach algebra of operators on such that . Diagonal algebras are employed in decomposing operator algebras into irreducible ones.

References

[1]	M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian)

Comments

In the article above, 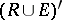denotes the commutant of the minimal closed symmetric algebra containing and .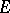

In Western terminology, a diagonal ring is called a diagonal algebra. The notion is due to T. Tomita [a1]. "Diagonal ring" only appears in the first edition of [1] and in the translations based on this edition. In the foreword to the second ( first revised) American edition (see [a2]), M.A. Naimark noted that "the theory of Tomita is valid only under the additional assumptions of separability type" and that he therefore preferred to give a discussion "which is closer to the initial simpler theory of von Neumann for the separable case" . For a different notion of diagonal algebra see, e.g., [a3].

References

[a1]	T. Tomita, "Representations of operator algebras" Math. J. Okayama Univ. , 3 (1954) pp. 147–173
[a2]	M.A. Naimark, "Normed algebras" , Wolters-Noordhoff (1972) (3rd American ed.)
[a3]	M. Takesaki, "Theory of operator algebras" , 1 , Springer (1979) pp. 259, 273