Omega-consistency

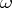-consistency

The property of formal systems of arithmetic signifying the impossibility of obtaining 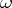-inconsistency. 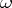-inconsistency is a situation in which, for some formula 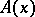, each formula of the infinite sequence 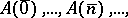and the formula 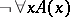are provable, where 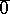is a constant of the formal system signifying the number 0, while the constants 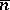are defined recursively in terms of 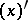, signifying the number following directly after : .

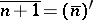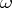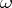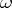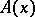The concept of -consistency appeared in conjunction with the Gödel incompleteness theorem of arithmetic. Assuming the -consistency of formal arithmetic, K. Gödel proved its incompleteness. The property of -consistency is stronger than the property of simple consistency. Simple consistency occurs if a formula not involving is taken as . It follows from Gödel's incompleteness theorem that there exist systems which are consistent but also 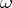-inconsistent.

References

[1]	S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951)