Fractional ideal
From Encyclopedia of Mathematics
A subset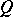 
of the field of fractions 
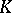of a commutative integral domain 
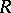of the form 
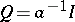, where 
, 
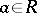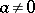, and 
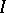is an ideal of 
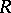. In other words, 
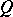is an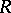 
-submodule of the field 
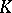all elements of which permit a common denominator, i.e. there exists an element 
, 
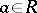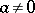, such that 
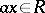for all 
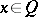. Fractional ideals form a semi-group 
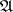with unit element 
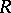with respect to multiplication. This semi-group is a group for Dedekind rings and only for such rings (cf. Dedekind ring). The invertible elements of the semi-group 
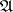are said to be invertible ideals. Each invertible ideal has a finite basis over 
.
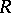References
| [1] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) |
| [2] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
'
How to Cite This Entry:
Fractional ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fractional_ideal&oldid=31616
Fractional ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fractional_ideal&oldid=31616
This article was adapted from an original article by L.A. Bokut (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article