Inter-quantile width

inter-quantile distance, inter-quantile range

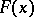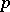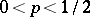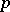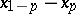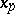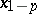The difference between the lower and upper quantiles of the same level (cf. Quantile). Let be a strictly-monotone continuous distribution function and let be an arbitrary number, . The inter-quantile distance at level is defined as , where and are the solutions of 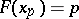and , respectively. Inter-quantile distances at well-chosen levels 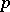are used in mathematical statistics and probability theory to characterize the dispersion (scatter) of probability distributions. E.g., the difference 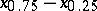, corresponding to , has the name inter-quartile distance, and in the case of a normal distribution it is equal to 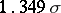(where 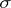is the natural measure of dispersion, called the standard deviation); half the inter-quartile (inter-decile) is called the probable deviation (probable error or semi-inter-quartile distance). If 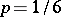or 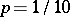, the inter-quantile distance is called the inter-sixtile or inter-tentile, respectively.

References

[1]	G.U. Yale, "An introduction to the theory of statistics" , Griffin (1916)