Wild imbedding
of a topological space 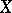 in a topological space
in a topological space 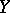
An imbedding which is topologically non-equivalent to an imbedding from a certain class of chosen imbeddings known as tame or nice imbeddings. The cases listed below are the most useful; the  -dimensional Euclidean space
-dimensional Euclidean space 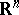 is taken as
is taken as 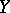 .
.
1) Let 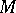 be a
be a 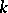 -dimensional topological manifold (cf. Topology of manifolds). A topological imbedding
-dimensional topological manifold (cf. Topology of manifolds). A topological imbedding 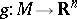 (cf. Topology of imbeddings) is called wild if there does not exist a homeomorphism of
(cf. Topology of imbeddings) is called wild if there does not exist a homeomorphism of  onto itself which would convert
onto itself which would convert 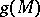 into a locally flat submanifold of
into a locally flat submanifold of 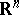 .
.
2) Let 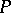 be a
be a 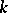 -dimensional polyhedron. A topological imbedding
-dimensional polyhedron. A topological imbedding  is called wild if there does not exist a homeomorphism of
is called wild if there does not exist a homeomorphism of 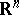 onto itself which would convert
onto itself which would convert 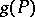 into a polyhedron (i.e. into a body having a certain triangulation) in
into a polyhedron (i.e. into a body having a certain triangulation) in 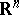 .
.
3) Let 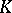 be a
be a 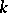 -dimensional locally compact space. A topological imbedding
-dimensional locally compact space. A topological imbedding 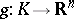 is called wild if there does not exist a homeomorphism of
is called wild if there does not exist a homeomorphism of 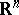 onto itself which would convert
onto itself which would convert 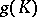 into a subset of the
into a subset of the 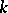 -dimensional Menger compactum
-dimensional Menger compactum 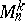 .
.
If the dimension 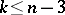 and if
and if 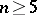 , then the properties introduced in all three cases are characterized by the following locally homotopic property: An imbedding is wild if and only if
, then the properties introduced in all three cases are characterized by the following locally homotopic property: An imbedding is wild if and only if 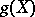 does not satisfy the property
does not satisfy the property 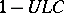 (cf. Topology of imbeddings). The situation is much more complicated for the codimensions
(cf. Topology of imbeddings). The situation is much more complicated for the codimensions 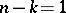 and
and  : The problem has been solved for manifolds of codimension 1 for
: The problem has been solved for manifolds of codimension 1 for 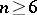 , but has not been fully solved for imbeddings of codimension 2 both for manifolds and for polyhedra. All that has been said is also meaningful if
, but has not been fully solved for imbeddings of codimension 2 both for manifolds and for polyhedra. All that has been said is also meaningful if 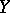 is an
is an  -dimensional manifold — topological or piecewise linear.
-dimensional manifold — topological or piecewise linear.
Wild imbedding. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wild_imbedding&oldid=31602