Bifactorial mapping
A mapping 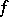 of a topological space
of a topological space 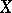 into a topological space
into a topological space 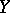 , in which for any covering of the inverse image
, in which for any covering of the inverse image 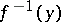 of any point
of any point 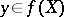 by sets open in
by sets open in 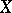 it is possible to select a finite number of sets so that
it is possible to select a finite number of sets so that 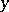 is located inside the image of their union. It is particularly important that the product of any collection of bifactorial mappings is a bifactorial mapping. Bifactorial mappings constitute an extensive class of factorial mappings, but nevertheless preserve the fine topological properties of spaces. Thus, continuous bifactorial
is located inside the image of their union. It is particularly important that the product of any collection of bifactorial mappings is a bifactorial mapping. Bifactorial mappings constitute an extensive class of factorial mappings, but nevertheless preserve the fine topological properties of spaces. Thus, continuous bifactorial  -mappings preserve a pointwise-countable base, and a factorial
-mappings preserve a pointwise-countable base, and a factorial  -mapping of a space with a pointwise-countable base onto a space of pointwise-countable type is bifactorial.
-mapping of a space with a pointwise-countable base onto a space of pointwise-countable type is bifactorial.
Bifactorial mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bifactorial_mapping&oldid=31588