E-number
From Encyclopedia of Mathematics
The limit of the expression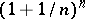 
as 
tends to infinity:
 |
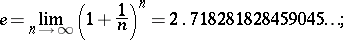it is the base for the natural logarithm. 
is a transcendental number, which was proved by C. Hermite in 1873 for the first time. Sometimes 
is called the Napier number for no very good reason.
Comments
See also Exponential function; Exponential function, real; Logarithm of a number; Logarithmic function; Transcendental number.
How to Cite This Entry:
E-number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=E-number&oldid=31585
E-number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=E-number&oldid=31585
This article was adapted from an original article by S.A. Stepanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article