Steiner curve
From Encyclopedia of Mathematics
A plane algebraic curve of order four, described by the point on a circle of radius  rolling upon a circle of radius
rolling upon a circle of radius 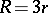 and having with it internal tangency; a hypocycloid with modulus
and having with it internal tangency; a hypocycloid with modulus 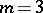 . A Steiner curve is expressed by the following equation in rectangular Cartesian coordinates:
. A Steiner curve is expressed by the following equation in rectangular Cartesian coordinates:
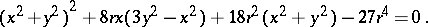 |
A Steiner curve has three cusps (see Fig. a).
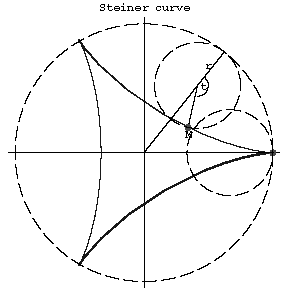
Figure: s087650a
The length of the arc from the point 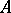 is:
is:
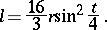 |
The length of the entire curve is 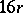 . The radius of curvature is
. The radius of curvature is 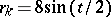 . The area bounded by the curve is
. The area bounded by the curve is 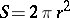 .
.
This curve was studied by Jacob Steiner (1798–1863).
References
| [1] | J. Steiner, "Werke" , 1–2 , Springer (1880–1882) |
Comments
References
| [a1] | M. Berger, "Geometry" , 1–2 , Springer (1987) pp. §9.14.34 (Translated from French) |
| [a2] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
How to Cite This Entry:
Steiner curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steiner_curve&oldid=31569
Steiner curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steiner_curve&oldid=31569
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article