Implicative normal form
From Encyclopedia of Mathematics
A propositional form of the type
 |
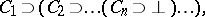where all the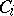 
, 
, have the form
 |
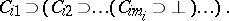Here, each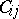 
(
; 
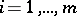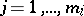) is either a variable or the negation of a variable, and 
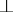is the logical symbol denoting falsehood. For each propositional formula 
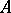one can construct an implicative normal form 
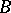classically equivalent to it and containing the same variables as 
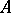. Such a 
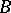is called an implicative normal form of 
.
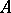References
| [1] | A. Church, "Introduction to mathematical logic" , 1 , Princeton Univ. Press (1956) |
How to Cite This Entry:
Implicative normal form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Implicative_normal_form&oldid=31564
Implicative normal form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Implicative_normal_form&oldid=31564
This article was adapted from an original article by S.K. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article