Quotient ring
of a ring  by an ideal
by an ideal 
The quotient group of the additive group of  by the subgroup
by the subgroup  , with multiplication
, with multiplication
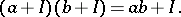 |
The quotient turns out to be a ring and is denoted by  . The mapping
. The mapping  , where
, where  , is a surjective ring homomorphism, called the natural homomorphism (see Algebraic system).
, is a surjective ring homomorphism, called the natural homomorphism (see Algebraic system).
The most important example of a quotient ring is the ring of residues modulo  — the quotient ring of the ring of integers
— the quotient ring of the ring of integers 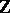 by the ideal
by the ideal 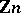 . The elements of
. The elements of 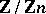 can be assumed to be the numbers
can be assumed to be the numbers 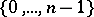 , where the sum and the product are defined as the remainders on diving the usual sum and product by
, where the sum and the product are defined as the remainders on diving the usual sum and product by  . One can establish a one-to-one order-preserving correspondence between the ideals of
. One can establish a one-to-one order-preserving correspondence between the ideals of  and the ideals of
and the ideals of  containing
containing 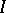 . In particular,
. In particular, 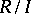 is simple (cf. Simple ring) if and only if
is simple (cf. Simple ring) if and only if 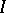 is a maximal ideal.
is a maximal ideal.
Comments
Another most important example is the quotient ring  , where
, where  is the ring of polynomials over
is the ring of polynomials over  in one variable
in one variable  and
and 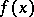 is an irreducible polynomial. This quotient ring describes all field extensions of
is an irreducible polynomial. This quotient ring describes all field extensions of 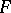 by roots of the equation
by roots of the equation  (cf. also Extension of a field).
(cf. also Extension of a field).
References
| [a1] | P.M. Cohn, "Algebra" , 1 , Wiley (1982) pp. Sect. 10.1 |
Quotient ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quotient_ring&oldid=31548