Unitary space

A vector space over the field of complex numbers, on which there is given an inner product of vectors (where the product 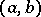of two vectors and is, in general, a complex number) that satisfies the following axioms:

1) ;

2) ;

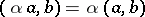3) ;

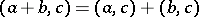4) if 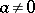, then 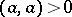, i.e. the scalar square of a non-zero vector is a positive real number.

A unitary space need not be finite-dimensional. In a unitary space one can, just as in Euclidean spaces, introduce the concept of orthogonality and of an orthonormal system of vectors, and in the finite-dimensional case one can prove the existence of an orthonormal basis.

References

[a1]	W. Noll, "Finite dimensional spaces" , M. Nijhoff (1987) pp. 338
[a2]	W.H. Greub, "Linear algebra" , Springer (1975) pp. Chapt. XI