Conical surface

cone

The surface formed by the movement of a straight line (the generator) through a given point (the vertex) intersecting a given curve (the directrix). A conical surface consists of two concave pieces positioned symmetrically about the vertex.

A second-order cone is one which has the form of a surface of the second order. The canonical equation of a real second-order conical surface is

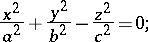if 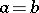, the surface is said to be circular or to be a conical surface of rotation; the canonical equation of an imaginary second-order canonical surface is

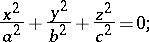the only real point of an imaginary conical surface is .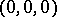

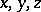An -th order cone is an algebraic surface given in affine coordinates by the equation

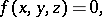where 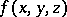is a homogeneous polynomial of degree (a form of degree in 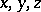). If the point 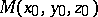lies on a cone, then the line 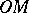also lies on the cone ( 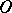is the coordinate origin). The converse is also true: Every algebraic surface consisting of lines passing through a single point is a conical surface.