Pi(number)

The ratio of the length of a circle to its diameter; it is an infinite non-periodic decimal number

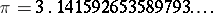One frequently arrives at the number as the limit of certain arithmetic sequences involving simple laws. An example is Leibniz' series

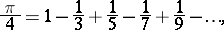which, however, converges very slowly. There are more rapidly-converging series suitable for calculating .

The possibility of a pure analytic definition of is of essential significance for geometry. For example, also participates in certain formulas in non-Euclidean geometry, but not as the ratio of the length of a circle to its diameter (this ratio is not constant in non-Euclidean geometry). The arithmetic nature of was finally elucidated in analysis, with a decisive part played by Euler's formula:

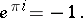At the end of the 18th century, J. Lambert and A. Legendre established that 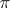is an irrational number, while in the 19th century, F. Lindemann showed that 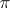is a transcendental number.

Comments

A nice account of Lindemann's proof can be found in [a3], Chapt. 6.

The number of known digits of 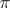has increased exponentially in recent times. At the moment (1990), the record seems to be half a billion digits (D.V. Chudnovsky and G.V. Chudnovsky). For an account of such computations see [a1]. Up to the 1960's the standard way to calculate 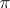was to use Machin's formula 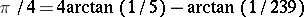and the power series of 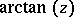. Nowadays, some powerful formulas of Ramanujan are used. It is still not known how randomly the digits of 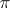are distributed; in particular, whether is a normal number.

References

[a1]	J.M. Borwein, P.B. Borwein, "Pi and the AGM" , Interscience (1987)
[a2]	P. Beckmann, "A history of pi" , The Golem Press , Boulder (Co.) (1971)
[a3]	I. Stewart, "Galois theory" , Chapman & Hall (1979)