Quadratic deviation

quadratic variance, standard deviation, of quantities from

The square root of the expression

(*)

The quadratic deviation takes its smallest value when , where 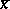is the arithmetic mean of :

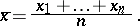In this case the quadratic deviation serves as a measure of the variance (cf. Dispersion) of the quantities . Also used is the more general concept of a weighted quadratic deviation:

where the are the so-called weights associated with . The weighted quadratic deviation attains its smallest value when is the weighted mean:

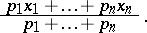In probability theory, the quadratic deviation 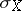of a random variable 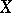(from its mathematical expectation) refers to the square root of its variance: .

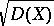The quadratic deviation is taken as a measure of the quality of statistical estimators and in this case is referred to as the quadratic error.

Comments

The expression (*) itself is sometimes referred to as the mean-squared error or mean-square error, and its root as the root mean-square error. Similarly one has a weighted mean-square error, etc.

References

[a1]	K. Rektorys (ed.) , Applicable mathematics , Iliffe (1969) pp. 1318
[a2]	A.M. Mood, F.A. Graybill, "Introduction to the theory of statistics" , McGraw-Hill (1963) pp. 166, 176