Axiom of extensionality
One of the axioms of set theory, asserting that two sets are equal if they contain the same elements:
 |
In a language not containing the equality symbol and having only one predicate symbol  , the axiom of extensionality has the form
, the axiom of extensionality has the form
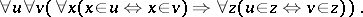 |
The axiom of extensionality has no real importance for the formalization of mathematics in the Zermelo–Fraenkel system  . Anything that can be constructed within the system
. Anything that can be constructed within the system  can be formalized in a system without the axiom of extensionality. Let
can be formalized in a system without the axiom of extensionality. Let  be the system obtained from
be the system obtained from  by removing the axiom of extensionality and by replacing formulas of the form
by removing the axiom of extensionality and by replacing formulas of the form  in the remaining axioms by the formula
in the remaining axioms by the formula
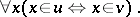 |
Then it can be shown that there exists an interpretation of 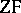 in
in 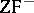 . A similar assertion is valid for the theory of types.
. A similar assertion is valid for the theory of types.
For Quine's system 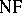 , obtained from the theory of types by the "erasure" of the type indices, the situation is different: It is not possible to interpret
, obtained from the theory of types by the "erasure" of the type indices, the situation is different: It is not possible to interpret  in
in  . The system
. The system 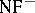 (
( without the axiom of extensionality) is a rather weak system, and its consistency can be proved in formal arithmetic. The system
without the axiom of extensionality) is a rather weak system, and its consistency can be proved in formal arithmetic. The system  , however, is not weaker than the theory of types with the axiom of infinity.
, however, is not weaker than the theory of types with the axiom of infinity.
References
| [1] | J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) |
| [2] | M. Boffa, "The consistency problem for NF" J. Symbolic Logic , 42 : 2 (1977) pp. 215–220 |
Comments
References
| [a1] | D.S. Scott, "More on the axiom of extensionality" Y. Bar-Hillel (ed.) E.I.J. Poznanski (ed.) M.O. Rabin (ed.) et al. (ed.) , Essays on the foundation of mathematics , North-Holland (1962) |
Axiom of extensionality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Axiom_of_extensionality&oldid=31424