Algebraic operation
 -ary operation, on a set
-ary operation, on a set 
A mapping
 |
of the  -th Cartesian power of the set
-th Cartesian power of the set  into the set
into the set  itself. The number
itself. The number  is known as the arity of the algebraic operation. Historically, the concepts of binary
is known as the arity of the algebraic operation. Historically, the concepts of binary  and unary (
and unary (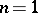 ) operations were the first to be considered. Nullary
) operations were the first to be considered. Nullary 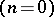 operations are fixed elements of the set
operations are fixed elements of the set 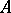 ; they are also known as distinguished elements or constants. In the 20th century the concept of an infinitary operation appeared, i.e. a mapping
; they are also known as distinguished elements or constants. In the 20th century the concept of an infinitary operation appeared, i.e. a mapping  , where
, where 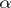 is an arbitrary cardinal number. A set with a system of algebraic operations defined on it is called a universal algebra.
is an arbitrary cardinal number. A set with a system of algebraic operations defined on it is called a universal algebra.
Comments
The study of infinitary operations actually started in the late 1950s [a1]. A nullary operation is also called a noughtary operation [a2].
References
| [a1] | J. Stominski, "The theory of abstract algebras with infinitary operations" Rozprawy Mat. , 18 (1959) |
| [a2] | P.M. Cohn, "Universal algebra" , Reidel (1981) pp. 13–14 |
Algebraic operation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_operation&oldid=31376