Lommel function
From Encyclopedia of Mathematics
A solution of the non-homogeneous Bessel equation
 |
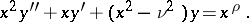If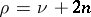 
, where 
is a natural number, then
 |
 |
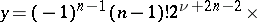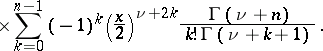If the numbers 
and 
are not integers, then
 |
 |
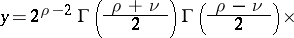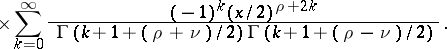If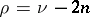 
, where 
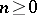is an integer and 
is not an integer 
, then
 |
 |
 |
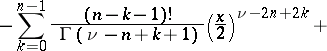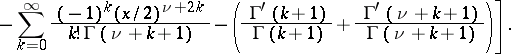Here, for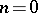 
the first sum is taken to be zero, and 
is a Bessel function (cf. Bessel functions). Lommel functions in two variables are also known.
See also Anger function; Weber function; Struve function.
Lommel functions were studied by E. Lommel [1].
References
| [1] | E. Lommel, "Zur Theorie der Bessel'schen Funktionen IV" Math. Ann. , 16 (1880) pp. 183–208 |
| [2] | G.N. Watson, "A treatise on the theory of Bessel functions" , 1 , Cambridge Univ. Press (1952) |
| [3] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1947) |
How to Cite This Entry:
Lommel function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lommel_function&oldid=31323
Lommel function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lommel_function&oldid=31323
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article