Casorati-Sokhotskii-Weierstrass theorem
Weierstrass theorem, Weierstrass–Sokhotskii–Casorati theorem
Let  be an essential singular point of an analytic function
be an essential singular point of an analytic function 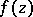 of a complex variable
of a complex variable  . Given any complex number
. Given any complex number 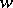 (including
(including 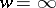 ), there is a sequence
), there is a sequence 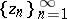 converging to
converging to  such that
such that
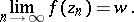 |
This theorem was the first result characterizing the cluster set 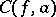 of an analytic function
of an analytic function 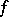 at an essential singularity
at an essential singularity  . According to the theorem,
. According to the theorem, 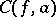 is total, that is, it coincides with the extended plane
is total, that is, it coincides with the extended plane 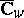 of the variable
of the variable 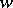 . The theorem was proved by Yu.V. Sokhotskii [1] (see also [2]). K. Weierstrass stated this theorem in 1876 (see [3]). Further information about the behaviour of an analytic function in a neighbourhood of an essential singularity is contained in the Picard theorem.
. The theorem was proved by Yu.V. Sokhotskii [1] (see also [2]). K. Weierstrass stated this theorem in 1876 (see [3]). Further information about the behaviour of an analytic function in a neighbourhood of an essential singularity is contained in the Picard theorem.
This theorem does not admit a direct generalization to the case of analytic mappings 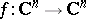 for
for 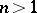 (see [5]).
(see [5]).
References
| [1] | Yu.V. Sokhotskii, "Theory of integral residues with some applications" , St. Petersburg (1868) (In Russian) |
| [2] | F. Casorati, "Teoria delle funzioni di variabili complesse" , Pavia (1868) |
| [3] | K. Weierstrass, "Zur Theorie der eindeutigen analytischen Funktionen" , Math. Werke , 2 , Mayer & Müller (1895) pp. 77–124 |
| [4] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [5] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) pp. Chapt. 2 (In Russian) |
Comments
In the West, this theorem is known universally as the Casorati–Weierstrass theorem. It was, however, proved earlier by C. Briot and C. Bouquet and appears in the first edition [a1] of their book on elliptic functions (1859), though it is missing from the second edition of this work; cf. the discussion in [a2], pp. 4–5.
References
| [a1] | C. Briot, C. Bouquet, "Théorie des fonctions doublement périodiques et, en particulier, des fonctions elliptiques" , Mallet–Bachelier (1859) |
| [a2] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 9 |
Casorati-Sokhotskii-Weierstrass theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Casorati-Sokhotskii-Weierstrass_theorem&oldid=31259