Essential singular point

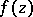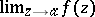An isolated singular point of single-valued character of an analytic function of a complex variable at which the limit , whether finite or infinite, does not exist. In a sufficiently small punctured neighbourhood 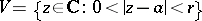of an essential singular point 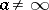, or 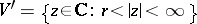in case , the function 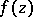can be expanded into a Laurent series:

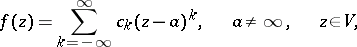or, correspondingly,

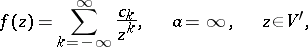where in the principal part of these series there is an infinite number of non-zero coefficients 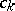with negative indices .

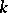The Sokhotskii theorem asserts that every complex value 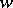in the extended complex plane 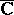is a limit value for the function 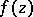in any neighbourhood, however small, of an essential singular point . According to the Picard theorem, every finite complex value 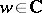, with one possible exception, is a value of 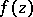taken infinitely often in any neighbourhood of an essential singular point . 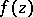The Sokhotskii theorem can also be expressed in another way, by stating that the cluster set of a function at an essential singular point coincides with the extended complex plane 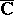. For regular points and poles, this set, on the other hand, is degenerate, i.e. it reduces to a single point 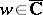. Therefore, in a more general sense, the name essential singular point of an analytic function 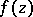is applied to every singular point (not necessarily isolated) at which no finite or infinite limit exists, or, in other words, at which the cluster set 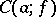is non-degenerate. The theorems of Sokhotskii and Picard for such essential singular points, not being isolated points of the set of all singular points, have only been proved under certain additional assumptions. For example, these theorems still hold for an isolated point of the set of essential singular points, in particular for a limit point of the poles of a meromorphic function.

A point 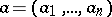of the complex space 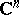, , is called a point of meromorphy of an analytic function 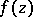of several complex variables if 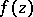is a meromorphic function in a neighbourhood of , i.e. if 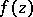can be represented in 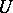as a quotient of two holomorphic functions: 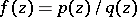, . Singular points of 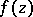that are not points of meromorphy are called essential singular points of 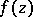. In these cases the non-degeneracy of the cluster set ceases to be a characteristic property of essential singular points.

References

[1]	A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian)
[2]	B.A. Fuks, "Introduction to the theory of analytic functions of several complex variables" , Amer. Math. Soc. (1965) (Translated from Russian)

Comments

In Western literature the Sokhotskii theorem is known as the Casorati–Weierstrass theorem.

References

[a1]	S. Saks, A. Zygmund, "Analytic functions" , Elsevier (1971) (Translated from Polish)