Cauchy kernel
From Encyclopedia of Mathematics
The function of the form  , which is the kernel of the Cauchy integral. In the case of the unit circle one has the following relationship between the Cauchy kernel and the Hilbert kernel:
, which is the kernel of the Cauchy integral. In the case of the unit circle one has the following relationship between the Cauchy kernel and the Hilbert kernel:
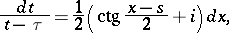 |
where
 |
The term Cauchy kernel is sometimes applied to the function
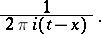 |
Comments
See also Kernel function; Kernel of an integral operator.
References
| [a1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1–3 , Chelsea (1977) (Translated from Russian) |
| [a2] | E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948) |
| [a3] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1974) pp. 24 |
How to Cite This Entry:
Cauchy kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_kernel&oldid=31229
Cauchy kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_kernel&oldid=31229
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article