Cauchy integral theorem

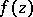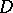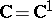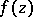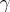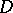If is a regular analytic function of a complex variable in a simply-connected domain in the complex plane , then the integral of along any closed rectifiable curve in vanishes:

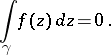An equivalent version of Cauchy's integral theorem states that the integral

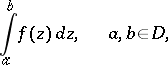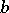is independent of the choice of the path of integration between the fixed points and in 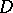. This, essentially, was the original formulation of the theorem as proposed by A.L. Cauchy (1825) (see [1]); similar formulations may be found in the letters of C.F. Gauss (1811). Cauchy's proof involved the additional assumption that the derivative 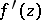is continuous; the first complete proof was given by E. Goursat [2]. The property of analytic functions expressed by the Cauchy integral theorem fully characterizes them (see Morera theorem), and therefore all the fundamental properties of analytic functions may be inferred from the Cauchy integral theorem.

For an arbitrary domain 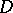in the plane 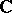or on a Riemann surface, the Cauchy integral theorem may be stated as follows: If 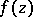is a regular analytic function in the domain 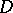, then the integral of 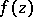along any rectifiable closed curve 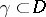which is homotopic to zero in 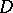vanishes.

A generalization of the Cauchy integral theorem to analytic functions of several complex variables is the Cauchy–Poincaré theorem: If 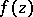, , 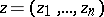is a regular analytic function in a domain 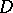of the complex space 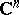, , 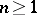then, for any 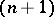-dimensional surface 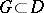with smooth boundary ,

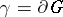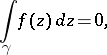where 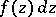is an abbreviation for the holomorphic differential form

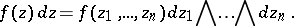When 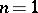the surface 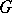and the domain 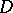have the same dimension, 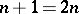(the case of the classical Cauchy integral theorem); when 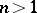, 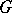has lower dimension than 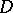, 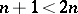. See also Residue of an analytic function; Cauchy integral.

References

[1]	A.L. Cauchy, "Oeuvres complètes, Ser. 1" , 4 , Paris (1890)
[2]	E. Goursat, "Démonstration du théorème de Cauchy" Acta Math. , 4 (1884) pp. 197–200
[3]	A.I. Markushevich, "Theory of functions of a complex variable" , 1–2 , Chelsea (1977) (Translated from Russian)
[4]	V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian)
[5]	B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian)

Comments

In [2] Goursat still assumed continuity of 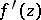. He soon saw how to remove this assumption, cf. [a1].

References

[a1]	E. Goursat, "Sur la définition générale des fonctions analytiques, d'après Cauchy" Trans. Amer. Math. Soc. , 1 (1900) pp. 14–16